From Micro to Macro: Uncovering and Predicting Information Cascading Process with Behavioral Dynamics
Linyun Yu$^1$, Peng Cui$^1$, Fei Wang$^2$, Chaoming Song$^3$, Shiqiang Yang$^1$
$^1$ Tsinghua University
$^2$ University of Connecticut
$^3$ University of Miami
Notice
Please use full-screen mode for better visual experience.
Introduction to Cascade
In network environment, if decentralized nodes act on the basis of how their neighbors act at earlier time, cascades will be formed.
Information cascade is ubiquitous
Social Media
Word-of-Mouth (Marketing)

Epidemics
Traffic
Cascading Process Prediction
-
Problem Definition:
- Source: the early stage of an information cascade
- Target: the later stage of the information cascade, or its cumulative cascade size of any later time
Cascading process
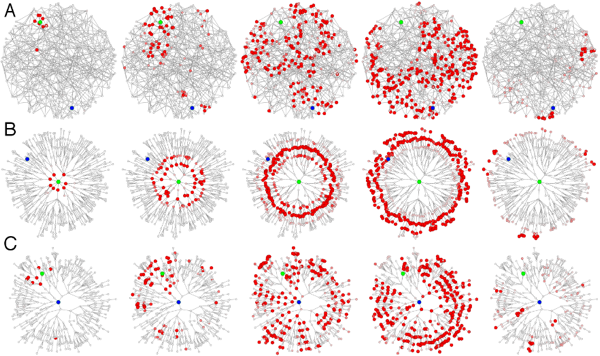
From Macro to Micro: Subcascades
- How to model subcascades?
- How to connect subcascades and cascade?
- How to make predictions quickly?
User Behavioral Dynamics
- Behavioral Dynamics of a user: The changing process of its offspring nodes that involve in the cascade after the user involved in the post.
-
Representation
-
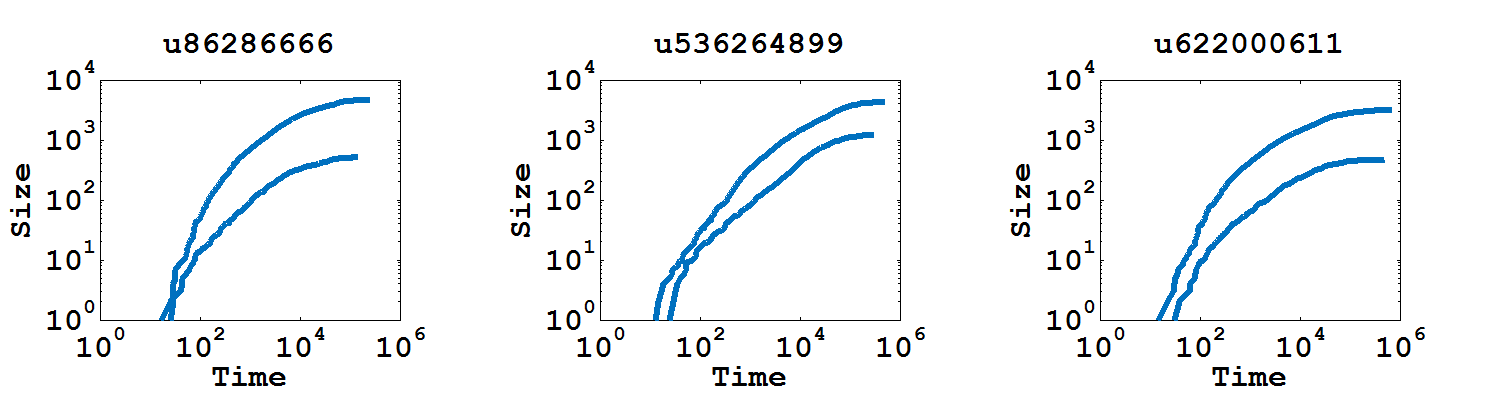
Averaging the size growth curve:
- Different subcascades of the same user might have different size growth curves.
-
Survival rate: the percentage of nodes that has not been but will be infected
- For different subcascades of the same user, the survival function is quite stable.
-
Averaging the size growth curve:
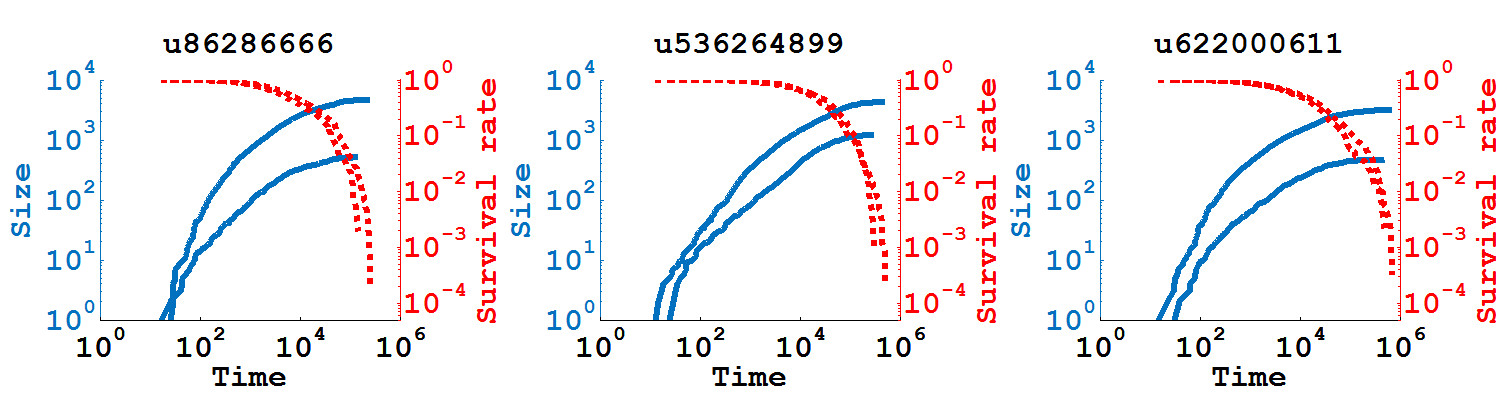
Parametrize Behavioral Dynamics
- The behavioral dynamics need to be parametrized for the ease of computation and modeling.
- Exponential and Rayleigh distributions cannot well capture both the shape and scale characteristics of behavioral dynamics.
-
The Weibull distribution is adequate for parameterizing behavioral dynamics:
- $\lambda$: control the scale parameter
- k: control the shape parameter
Covariates of Behavioral Dynamics
Interaction information between nodes is not always available. It is difficult to measure out-of-sample nodes.
The parameters of the user’s behavioral dynamics can be well estimated by the behavioral features of its network neighbors.
NEtworked WEibull Regression (NEWER)
Objective function:
min(
-Event log likelihood
+
Parameterizing$~\lambda$
+
Parameterizing$~k$
)
|
Event log likelihood:
|
Parameterizing$~\lambda$:
|
|
|
Parameterizing$~k$:
|
||
|
N: user number
$T_{i,j}$: the j-th event time to user i
$x_i$: feature vector for user i
|
Subcascade Process Prediction
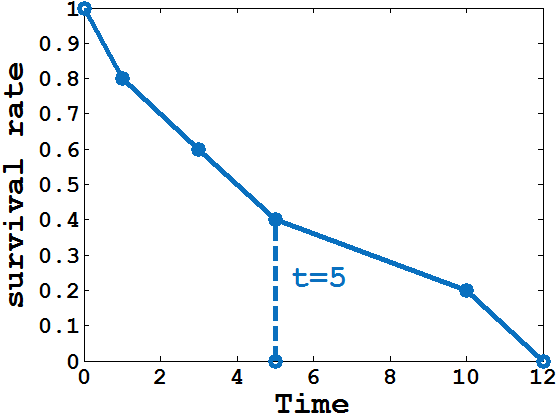
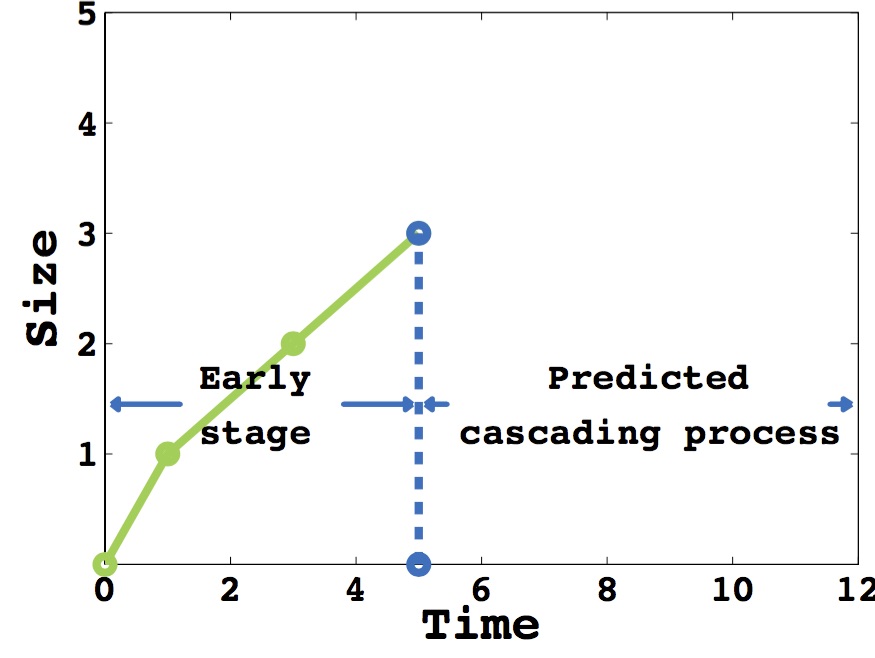
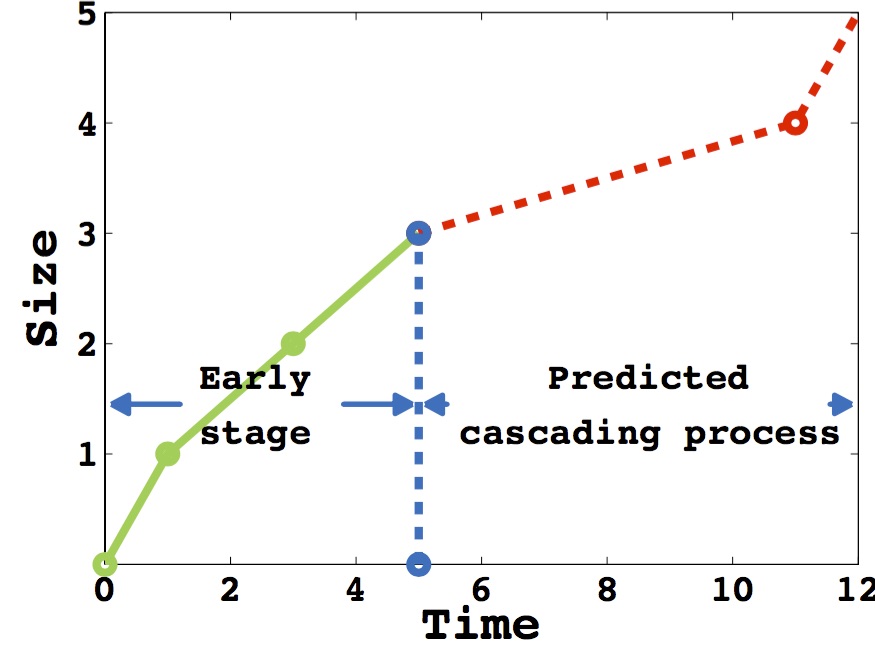
From rate dimension to size dimension
Base Model: From Subcascades to Cascade
Linking idea: Use all appeared subcascades to approximate the cascades
Problem: Will miss some unobserved subcascades
Minor dominance: Few nodes dominate the cascading process.
Earlystage dominance: Dominant nodes are prone to join early.
Cascading Process Prediction:
Dymamic Prediction
Real Application Demand:
- Accuracy
- Immediacy
From Base Model to Scalable Model:
-
Sampling strategies:
- Ignore most recalculations for subcascades.
- Setting the calculation time point based on the last calculations.
Experiments
-
Datasets: Tencent Weibo
- All cascades generated between Nov 15th and Nov 25th in 2011.
- retain all 0.59 million cascades that the cascades size are at least 5.
-
Baseline:
- Cox Proportional Hazard Regression Model (Cox)
- Exponential/Rayleigh Proportional Hazard Regression Model (Exponential/Rayleigh)
- log-Linear regression(Log-linear)
-
Evaluation metric:
- RMSLE: Root Mean Square Log Error
- ∆σ-Precision: Precision value that the predicted value within $(1 + σ)^{±1} groundtruth$
Cascade size prediction
What is the final size of the cascade?
Outbreak time prediction
When will the cascade break out?
Cascading Process Prediction
What is the size of the cascade at any later point?
Efficiency of the method
How fast can our method achieve?
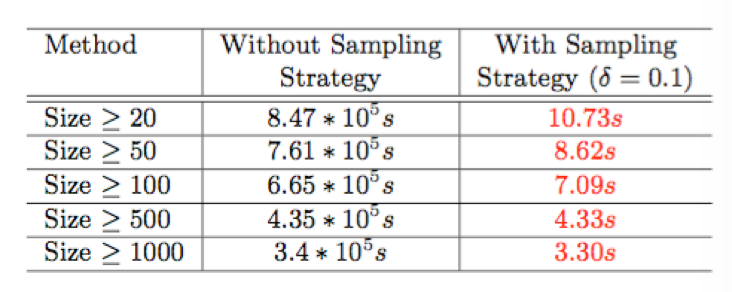
Running time for cascade size prediction
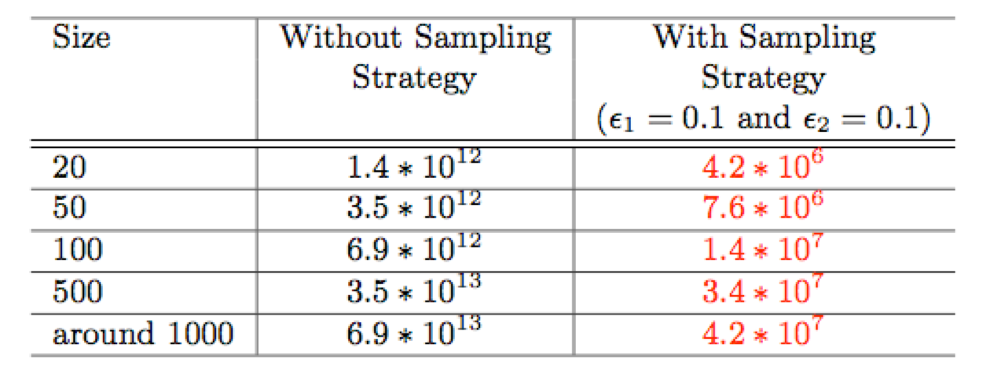
Calculation number for cascade process prediction
Conclusion
-
A new Problem:
- Given early stage information, predict the future cascading process.
-
A new angle:
- Uncover, model and predict the cascading process through behavioral dynamics.
-
A new model (NEWER):
- Model the behavioral dynamics and predict the subcascading process.
-
A scalable solution:
- Predict the dynamic process of information cascade with linear complexity.